这一章重点在于理解,而想要加深理解可以从两个方面入手:总结和练习。
本章的主要内容是:计算机中数的表示、计算机的运算方法和运算器的设计,学习这一章需要有点耐心。
无符号数和有符号数
无符号数
无符号数比较简单,寄存器的位数直接反映了无符号数的表示范围。实际上,有 C 语言基础的话,这是不言而喻的,就不再赘述了。
可能会有人有疑问:为什么没有无符号小数?
就笔者的个人理解而言,一是因为没有必要去专门使用无符号小数,二是因为小数在计算机中的表示本身就很麻烦了,在加上无符号号小数就更麻烦了。当然,具体的原因只能去问当初发明计算机的那帮老头子了。
有符号数
有符号数就比较复杂了,分为整数和小数,下面要介绍的各种表示法都是从这两个方面展开的。
机器数与真值
首先要明确的两个概念是:机器数与真值。
所谓机器数,简单理解就是计算机内存储的数,这个数跟现实中的数是存在差异的;而这里的真值不是true和false,只是现实中的有大小和正负的数,它可以是十进制的也可以是二进制的。
以下数学定义部分,$x$ 都为真值,$n$ 为整数或小数的位数。
原码表示法
包含两个部分:整数和小数。
整数
首先是定义:
$$
[x]_原 =
\begin{cases}
0,x & 2^n > x \geqslant 0 \\
2^n-x & 0 \geqslant x > -2^n \\
\end{cases}$$
比如:$x = +1110$,$[x]_原 = 0,1110$;$x = -1110$,$[x]_原 = 2^4 + 1110 = 1,1110$。实际上,$2^4$其实就是$10000$,写成指数形式更贴近定义中的公式,可千万别以为是新东西。
注意:上述默认机器字长是 5 位(后面的内容也都默认机器字长在合理范围内),逗号用来隔开符号位和数值部分。
小数
定义:
$$
[x]_原 =
\begin{cases}
x & 1 > x \geqslant 0 \\
1-x & 0 \geqslant x > -1 \\
\end{cases}$$
比如:$x = +0.1101$,$[x]_原 = 0.1101$;$x = -0.1101$,$[x]_原 = 1 - (-0.1101) = 1.1101$。
与上述一样,机器字长默认为 5 位,小数点用来隔开符号位和数值部分。
最后,还要把特殊的 0 单独拿出来讨论下,按照原码小数的定义,有:+0:$x = +0.0000,[+0.0000]_原 = 0.0000$-0:$x = -0.0000,[-0.0000]_原 = 1.0000$
同理,对于整数,就有:+0:$[+0]_原 = 0,0000$-0:$[-0]_原 = 1,0000$
综上,+0和-0的原码不同。
补码表示法
补码的概念有点类似于模运算中的补数,不复杂,但是日常生活中用的不多。
整数
定义:
$$
[x]_补 =
\begin{cases}
0,x & 2^n > x \geqslant 0 \\
2^{n+1}+x & 0 > x \geqslant -2^n (mod\ 2^{n+1})\\
\end{cases}$$
比如:$x = +1010$,$[x]_补 = 0,1010$;$x = -1011000$,$[x]_补 = 2^{7+1} + (-1011000) = 1,0101000$。
小数
定义:
$$
[x]_补 =
\begin{cases}
x & 1 > x \geqslant 0 \\
2+x & 0 > x \geqslant -1 (mod\ 2)\\
\end{cases}$$
比如:$x = +0.1110$,$[x]_补 = 0.1110$;$x = -0.1100000$,$[x]_补 = 2 + (-0.1100000) = 1.0100000$。
实际上,关于补码有一些规律:
- 正数的补码就是其本身
- 负数的补码可用其原码除符号位,每位取反,末位加 1 求得
同样,补码也存在 0 这个特殊情况,按照补码小数的定义:+0:$x = +0.0000,[+0.0000]_补 = 0.0000$-0:$x = -0.0000,[-0.0000]_补 = 1.0000$
同理,对于整数,就有:+0:$[+0]_补 = 0,0000$-0:$[-0]_补 = 1,0000$
综上,+0和-0的补码相同。
反码表示法
整数
定义:
$$
[x]_反 =
\begin{cases}
0,x & 2^n > x \geqslant 0 \\
(2^{n+1}-1)+x & 0 > x \geqslant -2^n (mod\ 2^{n+1}-1)\\
\end{cases}$$
比如:$x = +1101$,$[x]_反 = 0,1101$;$x = -1101$,$[x]_反 = (2^{4+1}-1) - 1101 = 1,0010$。
小数
定义:
$$
[x]_反 =
\begin{cases}
x & 1 > x \geqslant 0 \\
(2-2^{-n})+x & 0 \geqslant x > -1 (mod\ 2-2^{-n})\\
\end{cases}$$
比如:$x = +0.1101$,$[x]_反 = 0.1101$;$x = -0.1010$,$[x]_反 = (2-2^{-4} - 0.1010) = 1.0101$。
同样,反码也存在 0 这个特殊情况,按照反码小数的定义:+0:$x = +0.0000,[+0.0000]_补 = 0.0000$-0:$x = -0.0000,[-0.0000]_补 = 1.1111$
同理,对于整数,就有:+0:$[+0]_补 = 0,0000$-0:$[-0]_补 = 1,1111$
综上,+0和-0的反码不同。
小结
总结一下三种机器数的规律:
- 对于正数,原码 = 补码 = 反码
- 对于负数,符号位为 1,其原码除符号位外每位取反,末位加 1 可得补码;其原码除符号位每位取反,可得反码
移码表示法
补码无法直接判断两个符号不同的整数的大小关系,由此产生的就是移码。
移码定义:
$$
[x]_移 =
\begin{cases}
2^n+x & 2^n > x \geqslant -2^n \\
\end{cases}$$
比如:$x = 10100$,$[x]_移 = 2^5 + 10100 = 1,10100$;$x = -10100$,$[x]_移 = 2^5 - 10100 = 0,01100$。
实际上,移码与补码只差了一个符号位:正数的移码的符号位为 1,负数的移码的符号位为 0。最小真值的移码为全 0,同时+0和-0的移码也是相等的(与补码一致)。移码的用途就是用来表示浮点数的阶码,这样可以很方便的判断浮点数阶码大小。
数的定点表示和浮点表示
定点表示
按照小数点的位置有两种表示方法,一种是小数点在数符之后(小数定点机),另一种是小数点在数值之后(整数定点机),具体如下图:

浮点表示
引入浮点数的目的是为了方便科学计算,其一般形式为:
$$
N = S \times r^j
$$
其中,$S$ 为尾数,是数的小数部分,可正可负;$j$ 为阶码,是基值的指数部分,可正可负;$r$ 尾数的基值,也就是进制数。
具体来讲,在计算机存储的浮点数包含了五个部分,如下图:
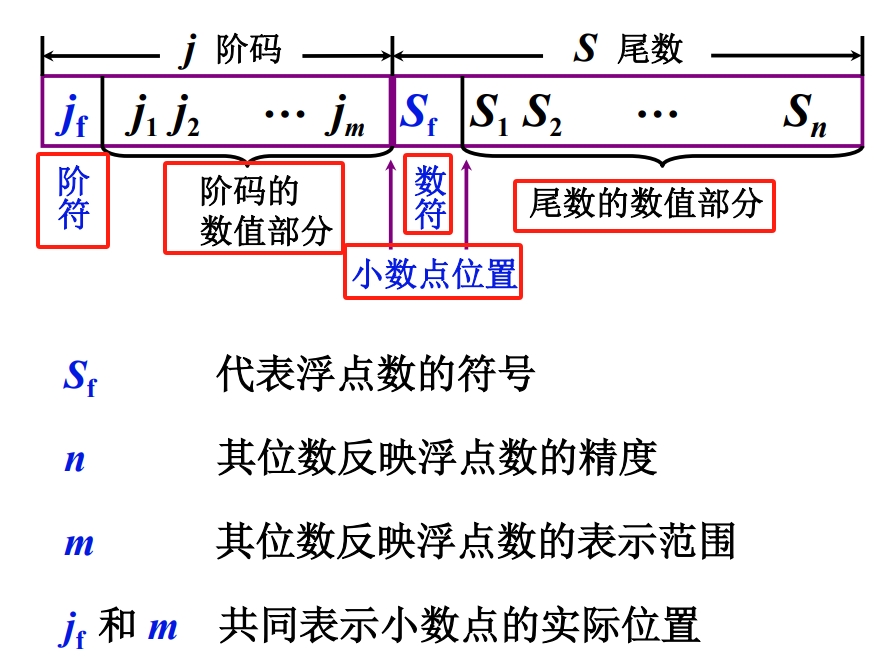
最后需要指出的是浮点数的表示范围,如下图:

注意上图中的范围,发生下溢时,按照机器零处理;发生上溢时,按照计算出错处理。
总结
总体来说,这章的内容不难,但是很繁琐,只是需要做好区分和总结。
然后是这一章的思维导图:
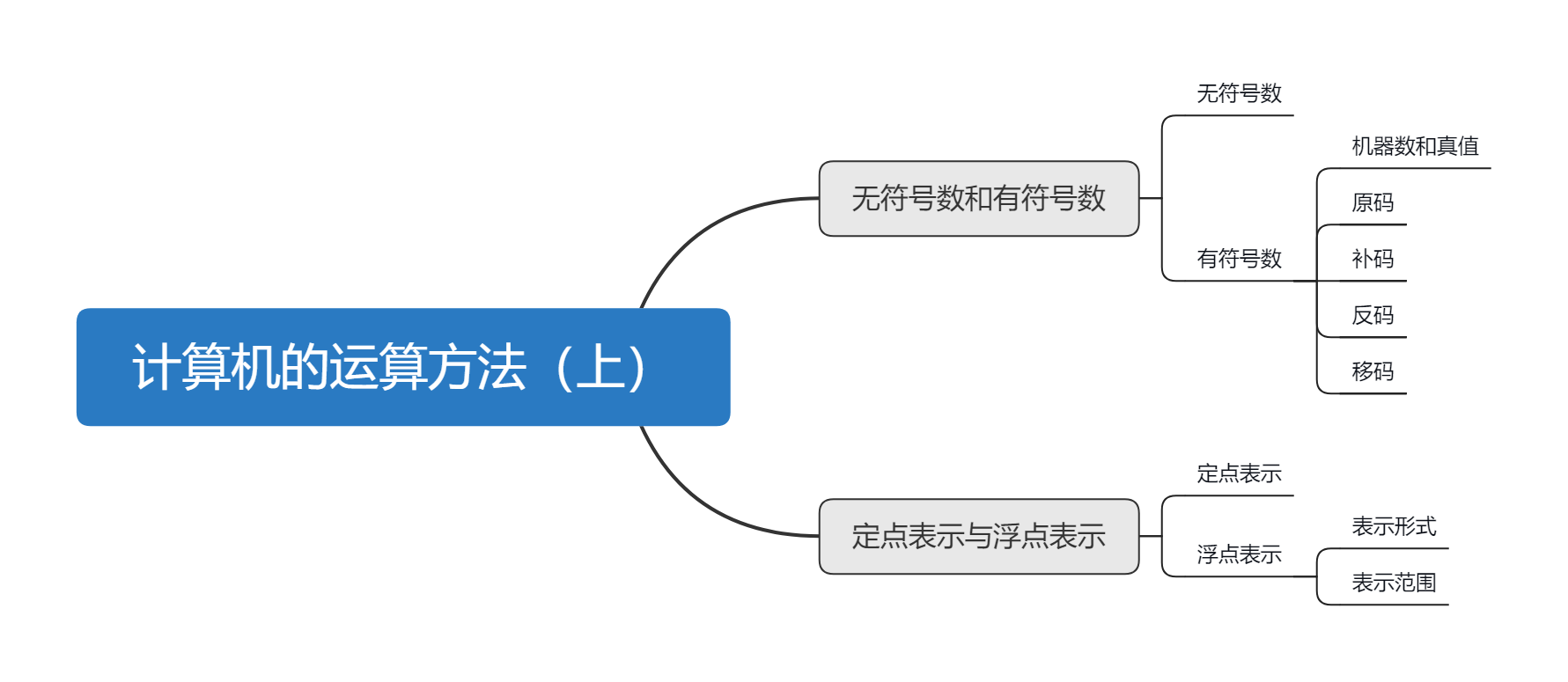
PS:光看图的话,内容确实不多...

