ZJU_DS_12-KMP

Posted on | Edited on | In ,
| 4.9k | 41 mins.

本周主要讲解几道题目，然后再介绍一下 KMP 算法。

串

在了解KMP算法之前，我们先了解一下什么是串。
串（String）其实也是线性表的一种应用，指的是线性存储的一组数据（常见是字符，正所谓“字符串”），当然，串不仅仅包含字符，它是通用的数据结构。同时，与串相关的操作集有很多，如：求串的长度、比较两串是否相等、两串相接、求子串、插入子串、匹配子串（KMP 就是干这事的）、删除子串等。

KMP

匹配子串

什么是“匹配子串”呢？看名字，其实有两个着重点，一个是匹配，一个是子串。举个例子，给定一段文本，从中找出某个指定的关键字，例如给定文本：This is not a bug, it’s destiny. ，需要从中找出 bug 这个关键字（当然这并不是件复杂的事情），这实际上就是“匹配子串”。

那么我们重新规范一下，就是：给定一个文本：string = xxxxxxx，在给定一个模式：pattern = xxxx，求 pattern 在 string 中出现的位置。

分析

依据匹配子串的思路，如果要找pattern在string中出现的位置，分别使用两个指针，接着对string进行遍历，同时与pattern逐个字符进行比较，如果出现不相等的，则string的指针回退到初试比较位置的后一个位置（若从 i 开始比较，则回退到 i+1 开始比较），pattern的指针则回退到第一位，重复执行即可，这实际上是一种暴力解法。
使用暴力解法时，串中肯定会有相同的序列存在，所以指针回溯后再次遍历比较时，就会进行重复的比较操作了，这样就做了很多无用的操作，而 KMP 算法就是用来解决这个问题的。

匹配函数

KMP 算法在直接进行匹配前会对模式串（pattern）进行分析，借助一个辅助数组match[]，这个数组内保存着模式串按照下面的 $ match $ 函数计算的“值”，根据这些“值”，再构造合适的判断规则来解决这个问题；match[]数组的下标就是模式串每一个字符的下标。
先来看一下这个 $ match $ 函数:

$$
match(j) = \begin{cases}
&\text{满足}p_0 \cdots p_i = p_{j-i} \cdots p_j \text{的最大}i(\lt j) \\
&-1\ \ \ \text{如果这样的} i \text{不存在}\end{cases}
$$

假设pattern为abcabcacab这个序列，下面来计算一下其由 $ match $ 函数得来的数组。

先从a开始，a为首字符，根据 $ match $ 函数的规则，match(0) = -1

继而到b，b需要和前面的a进行比较，发现不匹配，match(1) = -1

再看c，此时对于match函数而言，i可以取两个值，分别是0和1（此时j=2），取0时，c直接和a比较，不匹配，取1时，那就是ab和bc进行比较，还是不匹配，所以match(2) = -1

再看下一个a，此时i可以取三个值（0、1、2，注意match函数的条件是不大于j的最大i），取0，a和a比较，匹配成功，match(3) = 0，取1，ab和ca不匹配，取2，abc和bca也不匹配（若此时匹配，match(3)的值需要更新），所以match(3) = 0

按照这种思路，重复直至结束。


重复计算后，可以得到下表：

pattern a b c a b c a c a b
j 0 1 2 3 4 5 6 7 8 9
match -1 -1 -1 0 1 2 3 -1 0 1

match函数有多种和不同的称呼，有些书也叫next。另外，需要明确的是，这个特定函数的针对对象是pattern，也即是给定的模式串，而不是原串。另外，pattern比较短，string比较长，KMP算法只用分析一个短的子串而不用分析一个长串，这其实已经提升了效率。

算法实现

使用 $ match $ 函数获得match[]数组后，如何去使用match[]数组又成为新问题。
首先我们已经知道了，根据match[]数组可以避免去比较重复的序列，当不匹配时，指向pattern的指针p会去找p-1这个指针所指位置的match[]值，而这个match[]值加1就是指针p重新开始进行匹配的位置，即如下图所示：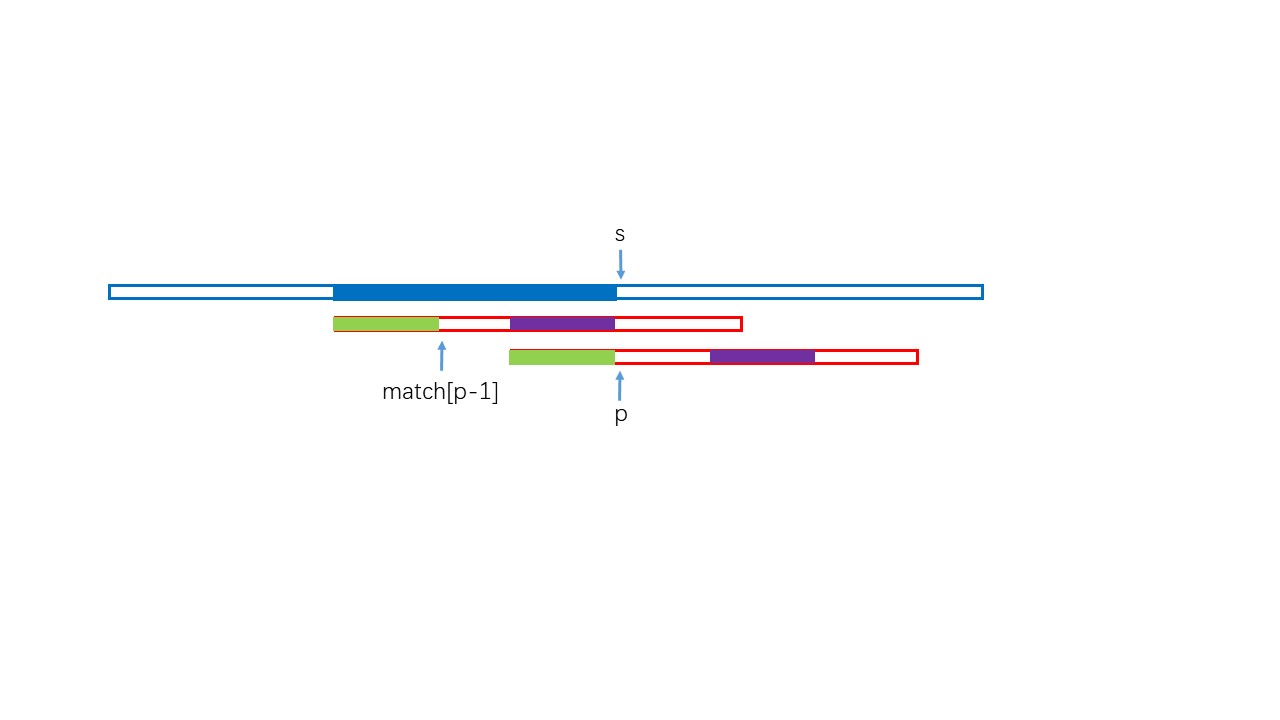
KMP
就是这样去使用match数组的，明确这个问题后，基本可以写出 KMP 算法的代码了，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Position KMP(char *string, char *pattern) {
    int n = strlen(string);	/* O(n) */
    int m = strlen(pattern);	/* O(m) */
    int s, p, *match;
    if(n < m) return NotFound;
    match = (int*)malloc(m*sizeof(int));
    BuildMatch(pattern, match);    /* T(B) */
    s = p = 0;
    while(s<n && p<m) {	 /* O(n) */ 
        if(string[s] == pattern[p]) {
            s++;
            p++;
        } else if(p > 0) p = match[p-1] + 1;
        else s++;
    }
    return (p==m)?(s-m):NotFound;
}

从上面的代码可以分析出其时间复杂度基本为$T = O(n+m) + T(B)$，BuildMatch函数的时间复杂度取决于其自身的实现方式，别忘记了，KMP是以它为前提的。

有了前面对 $ match $ 函数的分析，BuildMatch函数的构造就比较简单了，但若只是简单用线性的方法去构造match数组的话，会使得时间复杂度为$O(m^3)$，这就很不友好了，那怎么办呢？

答案是利用match[]数组内的值，如果是计算第i个位置的match值，那么必定得去找i-1的match值加1所指位置的字符是否与i所指位置的字符相同，如果相同，皆大欢喜，match[i] == match[i-1] + 1了，如果不相等呢？

就得去找i-1的match值的match值加1所指位置的字符是否与i所指位置的字符相同了（好绕...😓），也即match[match[i-1]]，若相同，match[i] == match[match[i-1]] + 1，如果还不相等，继续找吧...（还好是电脑干活😓）。
可参考下图：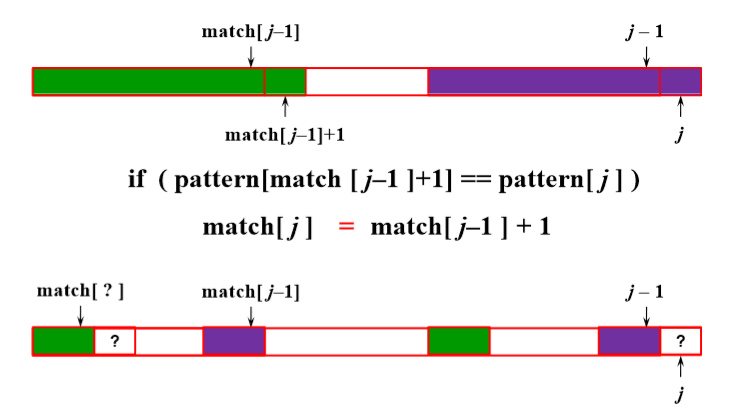
match_array
基本代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void BuildMatch(char *pattern, int *match) {
    int i, j;
    int m = strlen(pattern);	/* O(m) */
    match[0] = -1;
    for(j=1; j<m; j++) {	/* O(m) */
        i = match[i-1];
        while(i >= 0 && (pattern[i+1] != pattern[j])) {
            i = match[i];
        }
        if(pattern[i+1] == pattern[j]) {
            match[j] = i+1;
        } else match[j] = -1;
    }
}

简单分析一下上述代码的时间复杂度，可得 $T_m(N) = O(m)$，综合起来 KMP 算法的时间复杂度就是 $T(N) = O(n+m)$，从暴力解法的 $O(n·m)$ 优化成 $O(n+m)$，确实厉害！

Homework

串的模式匹配

这道题目是用来测试各式各样的串的模式匹配算法的，按照姥姥给出的代码，可以得到下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define NotFound -1
typedef int Position;

void Build_Match(char *pattern, int *match) {
    Position i, j;
    int m = strlen(pattern);
    match[0] = -1;
    for(j=1; j<m; j++) {
        i = match[j-1];
        while(i >= 0 && (pattern[i+1] != pattern[j])) {
            i = match[i];
        }
        if(pattern[i+1] == pattern[j]) match[j] = i+1;
        else match[j] = -1;
    }
}

Position KMP(char *string, char *pattern) {
    int n = strlen(string);
    int m = strlen(pattern);
    Position s, p, *match;
    if(n < m) return NotFound;
    match = (Position*)malloc(m*sizeof(Position));
    Build_Match(pattern, match);
    s = p =0;
    while(s<n && p<m) {
        if(string[s] == pattern[p]) {
            s++;
            p++;
        } else if(p > 0) p = match[p - 1]+1;
        else s++;
    }
    return (p == m) ? (s - m) : NotFound;
}

int main(int argc, char const *argv[]) {
    char string[] = "This is a simple example.";
    char pattern[] = "simple";
    Position p = KMP(string, pattern);
    if(p == NotFound) printf("Not Found.\n");
    else printf("%s\n", string+p);
    return 0;
}

/*
samples:
in:
abcabcabcabcacabxy
3
abcabcacab
cabcabcd
abcabcabcabcacabxyz

out:
abcabcacabxy
Not Found
Not Found 
*/

Buy me a coffee ? :)
0%