ZJU_DS_08-图（下）

Posted on | Edited on | In ,
| 12k | 1:38

这周课程主要介绍了图的另外两个应用：最小生成树和拓扑排序，顺带讲了一下关键路径

最小生成树

什么是最小生成树（Minimum Spaning Tree）？
它首先是一棵树，所以它没有回路，且 V 个顶点的最小生成树一定有 V-1 条边（这就是树的性值）。既然是生成树，所以这棵树包含了图中所有顶点，树中的 V-1 条边一定也都在图内；那最小是什么？最小的含义是指边的权重和最小。
这里要注意，如果图是连通的，那么这个图一定存在最小生成树且不一定唯一。

下面介绍的两种生成最小生成树的算法本质思想都是基于“贪心”，这与前面的 Dijkstra 算法是一致的。所谓“贪心”，即是指每一步都要“最好”的，在最小生成树中，权重最小的边也就是“最好”的了。

Prim 算法

Prim 算法的大致过程从一个顶点开始，慢慢的生长成一棵树，先看下它的伪码描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void Prim() {
    MST = {S};
    while(1) {
        V = 未收录顶点中 dist 最小者;
        if(V 不存在) break;
        将 V 收录进 MST;
        dist[V] = 0;
        for(V 的每个邻接点 W) {
            if(dist[W] != 0) {
                if( 边权(V,W) < dist[W]) {
                    dist[W] = 0;
                    parent[W] = V;
                }
            }
        }
    }
    if(MST 中收录的顶点不到 |Ｖ| 个) 
        Error("生成树不存在");
}

Prim 算法与 Dijkstra 算法十分类似，就是循环内的判断条件不一样，其他基本一致。以下图为例，手动模拟一下 Prim 算法的运行过程。dist 数组用来筛选边权最小的顶点；parent 数组来保存树，且 parent 数组需要初始化为 -1，这里与并查集的思路是类似的。

Graph_1

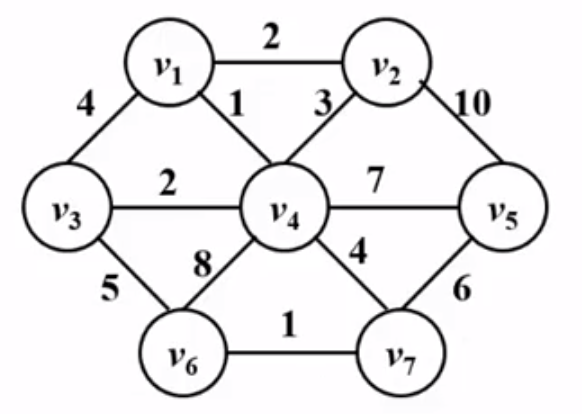
以$v_1$为源点，dist 数组初始化：

index 1 2 3 4 5 6 7
dist 0 ∞ ∞ ∞ ∞ ∞ ∞
parent -1 -1 -1 -1 -1 -1 -1

直接将 dist[1] 初始化为 0，然后$v_1$作为未收录顶点中 dist 最小者，将其收录进 MST，再访问其每个邻接点，此时可以将 dist 数组的值更新：

index 1 2 3 4 5 6 7
dist 0 2 4 1 ∞ ∞ ∞
parent -1 1 1 1 -1 -1 -1

接着，未收录顶点中 dist 最小者就是$v_4$，收录进 MST，此时 dist 和 parent 数组更新：

index 1 2 3 4 5 6 7
dist 0 2 2 0 7 7 4
parent -1 1 4 1 4 4 4

可以看到，因为$(v_4, v_3) < (v_1, v_3)$，所以 dist[3] 与 parent[3] 的值将会得到更新。

再来，未收录顶点中 dist 最小者就是$v_2$，收录进 MST，此时 dist 和 parent 数组更新：

index 1 2 3 4 5 6 7
dist 0 0 2 0 7 8 4
parent -1 1 4 1 4 4 4

依次类推，收录$v_3$，有：

index 1 2 3 4 5 6 7
dist 0 0 0 0 7 5 4
parent -1 1 4 1 4 3 4

收录$v_7$，有：

index 1 2 3 4 5 6 7
dist 0 0 0 0 6 1 0
parent -1 1 4 1 7 7 4

最后再分别选取$v_6$和$v_5$后，MST 中收录的顶点达到 |V| 个后就得到了最小生成树。通过上面也可以看出，Prim 中的 dist 数组的用途与 Djikstra 算法中 dist 数组的用途是完全一致的，只是两者的判断条件不一样而已。另外，Prim 算法的时间复杂度也就是$O(|V|^3)$。

Kruskal 算法

Kruskal 算法的大致过程是在“选边”，也就是将森林合并成树，其伪码描述为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Kruskal(Graph G) {
    MST = {};
    while(MST 中找不到 |V|-1 条边 && E 中还有边) {
        从 E 中取一条权重最小的边 E(v, w);	//使用最小堆实现
        将取出的最小边 E(v, w)从 E 中删除;
        if(E(v, w) 不在 MST 中构成回路) {		//使用并查集实现
            将 E(v, w)加入 MST;
        } else {
            彻底无视 E(v, w);
        }
    }
    if(MST 中找不到 |V|-1 条边) {
        Error("生成树不存在");
    }
}

以下图为例，手动模拟一下 Kruskal 算法的运行过程。

Graph_1

依次加入边$(v_1, v_4)$、$(v_6, v_7)$、$(v_1, v_2)$、$(v_3, v_4)$、$(v_4, v_7)$、$(v_5, v_7)$即可，整个过程讲起来比 Prim 算法简单了不少，但是实现起来就稍微复杂一点，既要用到最小堆，又要用到并查集，但其时间复杂度也稍微优秀一点（相比 Prim），为：$O(|E|Log|E|)$。另外，笔试题中，Kruskal 算法解题速度是第一名，谁用谁知道。

拓扑排序

拓扑排序不同于普通排序，普通排序就是按照某一规则对具有同类性质的元素进行升序或降序排序；而拓扑排序是针对有向无环图（Directed Acyclic Graph，DAG）G 进行的，是将图 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边 $<u, v>$是图 G 的边（也即存在一条 u 到 v 的有向路径），则 u 在线性序列中一定出现在 v 之前，这样的序列叫做拓扑序列，而这个得到这个序列的过程就叫做拓扑排序。

而姥姥讲的 AOV 网，具体定以请点击链接参考下百度百科。另外，对于一个 AOV 网而言，如果有合理的拓扑序，则其必定是有向无环图。换句话说，也就是说拓扑排序可以用来检测图内是否有环，这也是笔试题中常用的知识点。

拓扑排序的伪码算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void TopSort() {
    for(图中每个顶点 V) {
        if(Indegree[V] == 0) {
            Enqueue(V, Q);
        }
    }
    while(!IsEmpty(Q)) {
        V = Dequeue(Q);
        输出V，或者记录 V 的输出序号; cnt++;
        for(V 的每个邻接点 W) {
            if(--Indegree[W] == 0) {
                Enqueue(W, Q);
            }
        }
    }
    if(cnt != |V|) {
        Error("图中有回路");
    }
}

关键路径

关键路径问题是针对 AOE（Activity On Edge）网络而言的，属于拓扑排序的应用，一般用于安排项目的工序问题，图中的边代表工序，工序与工序之间有先后关系。也可以理解为边代表活动，顶点表示这个活动的结束，按照姥姥 PPT 中的介绍来理解即可，如下图所示：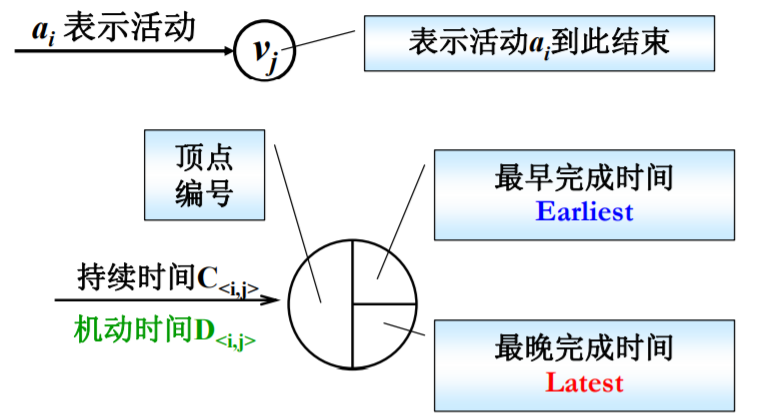
Critical_Path_1

接着跟着姥姥的 PPT 一起手动计算关键路径，可以得到下图的结果。

Critical_Path_2
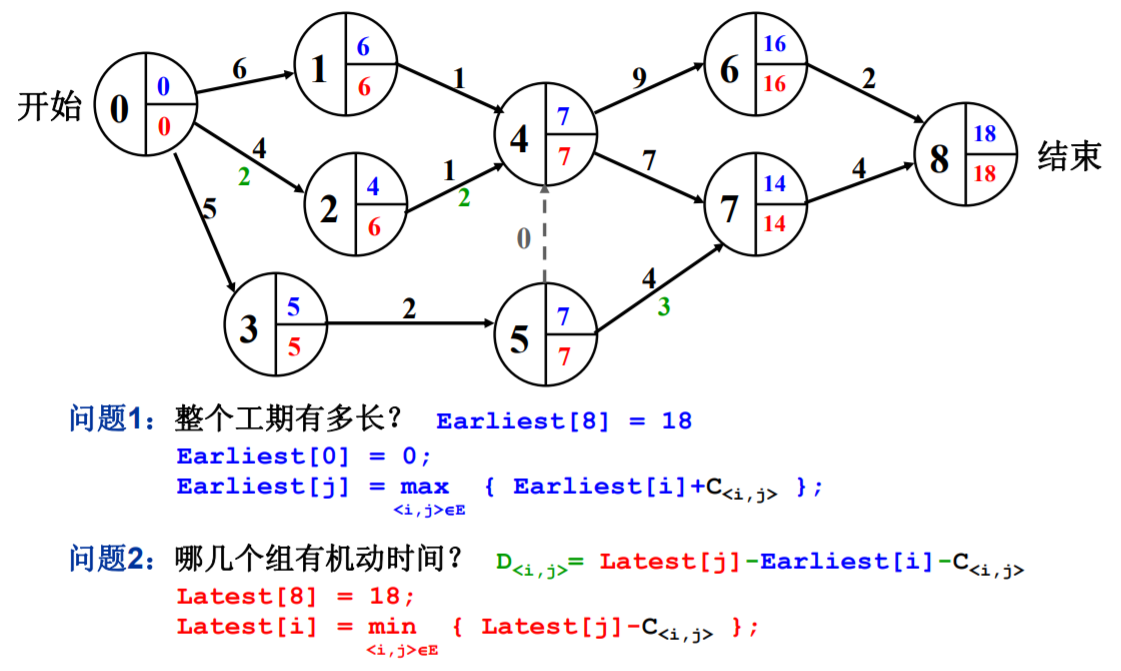
在上面的问题中，注意对那条“虚边”的理解，之所以会有这条虚边，其实是因为要想到达顶点 7，必须要先到达顶点 4 和 5。可能有人会问为什么是从 5 指向 4，很简单，因为 4 后到达，5 会先到达，如果 5 后到达，4 先到达，那就是 4 指向 5 了。

另外需要注意的就是机动时间的计算，还是要先理解机动时间的概念。机动时间这个东西，实际上就是可以偷懒的时间，后完成的人不能偷懒，但先完成的人就可以偷懒了。以顶点 5 为例，它的机动时间就是：$D_{<5, 7>} = Latest[7] - Earliest[i] - C_{<5, 7>} = 14 - 7 - 4 = 3$。会算这些东西后，就可以找出关键路径了，值得注意的是对一个 AOE 网而言，关键路径不一定是唯一的，这个从上图就可以看出。

Homework

08-7 公路村村通

很直观的最小生成树问题，一遍 Prim 算法就搞定了，如果不连通就输出 -1，反之就输出最小生成树的边权之和，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdbool.h> 
#define maxn 1005
const int inf = 0x3fffffff;
int nv, ne, G[maxn][maxn], dist[maxn];
bool visited[maxn] = { false };
void init() {
    for (int i = 0; i < maxn; i++) {
        for (int j = 0; j < maxn; j++) {
            G[i][j] = inf;
        }
    }
}
void prim() {
    for (int i = 0; i < maxn; i++) dist[i] = inf;
    dist[1] = 0;
    int times = 0, totalweight = 0;
    while(1) {
        int mindis = inf, v = -1;
        for (int i = 1; i <= nv; i++) {
            if (!visited[i] && dist[i] < mindis) {
                mindis = dist[i];
                v = i;
            }
        }
        if (v == -1) break;
        times++;
        visited[v] = true;
        totalweight += dist[v];
        for (int w = 1; w <= nv; w++) {
            if (G[v][w] != inf && !visited[w] && G[v][w] < dist[w]) {
                dist[w] = G[v][w];
            }
        }
    }
    if (times == nv) printf("%d", totalweight);
    else printf("-1");
}
int main() {
    scanf("%d %d", &nv, &ne);
    init();
    int v1, v2, weight;
    for (int i = 0; i < ne; i++) {
        scanf("%d %d %d", &v1, &v2, &weight);
        G[v1][v2] = G[v2][v1] = weight;
    }
    prim();
    return 0;
}

/*
samples:
in:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
out:
12

*/

08-8 How Long Does It Take

这道题虽然是英文的，但是题意很直观，就是直接求关键路径的最早完成时间，但实际上并没有要求也要输出关键路径，减少了点麻烦吧。解决这个问题的思路就是利用先拓扑排序，得到一个拓扑序列，然后通过这个拓扑序列来关键路径的最早完成时间。我们使用 STL 来偷下懒，将 Vector 当作邻接表来存储图，利用 Vector 内的成员函数 emplace_back（C++11 的新特性）来输入顶点和对应的边权要方便一些，但要这样用得先写好 node 的构造函数。
在进行拓扑排序时，可以顺便将最早完成时间也一并计算出来。为了避免图可能不是连通的，也就是说此时是无解的，需要设置一个计数器来记录所得到的拓扑序列的顶点个数，如果与图的顶点总数不相等，那也就是说图是不连通的。
具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int maxn = 100 + 5;
const int inf = 0x3fffffff;
struct node{
    int w, weight;
    node(int w, int weight) {
        this->w = w;
        this->weight = weight;
    }
};
vector<node> G[maxn];
int nv, ne, indegree[maxn] = { 0 }, cost[maxn];
void topsort() {
    queue<int> q;
    for (int v = 0; v < nv; v++) {
        for (int w = 0; w < G[v].size(); w++) {
            indegree[G[v][w].w]++;
        }
    }
    for (int i = 0; i < maxn; i++) cost[i] = -1;
    int count = 0;
    for (int i = 0; i < nv; i++) {
        if (indegree[i] == 0) {
            q.push(i);
            cost[i] = 0;
        }
    }
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        count++;
        for (int w = 0; w < G[v].size(); w++) {
            indegree[G[v][w].w]--;
            if (cost[G[v][w].w] < cost[v] + G[v][w].weight) {
                cost[G[v][w].w] = cost[v] + G[v][w].weight;
            }
            if (indegree[G[v][w].w] == 0) {
                q.push(G[v][w].w);
            }
        }
    }
    if (count != nv) cout << "Impossible";
    else {
        int max = cost[0];
        for (int i = 1; i < nv; i++) {
            if (max < cost[i]) max = cost[i];
        }
        cout << max;
    }
}
int main() {
    cin >> nv >> ne;
    int v1, v2, weight;
    for (int i = 0; i < ne; i++) {
        cin >> v1 >> v2 >> weight;
        G[v1].emplace_back(v2, weight);
    }
    topsort();
    return 0;
}

/*
samples:
in:
9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
out:
18

in:
4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5
out:
Impossible

in:
7 6
0 3 2
3 4 2
1 2 3
2 4 2
4 5 3
4 6 2
out:
8
*/

08-9 关键活动

这道题没啥说的，就是关键路径的问题。相比上道题，这道题要麻烦一些，因为这个题不仅要输出最早完成时间，还得输出关键路径，多亏了 STL 省了很多麻烦。
求最早完成时间的思路与上面那题是一样的，直接一个拓扑排序就完事了。难点在于如何找关键路径，不能简单的直接拿拓扑序列来反向输出，那怎么办呢？
仔细回忆一下课上的例子，可以发现关键路径的关键活动没有空余时间，假如 e 是活动的最早完成时间，l 是活动的最晚开始时间，那么关键活动的 e 与 l 是相等。按照这样的思路，将拓扑序列中的所有的关键活动的 e 和 l 求出，并进行比较，如果相等，就是关键活动了，当然了，前提是拓扑序列是存在的。
但是别忘记了，题目要求从小到大输出关键活动，所以还需要对找出的序列进行排序，然后再输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
using namespace std;
const int maxn = 100 + 5;
const int inf = 0x3fffffff;
struct node {
    int v, w;
    node(int v, int w) {
        this->v = v;
        this->w = w;
    }
};
bool cmp(int a, int b) {
    return b - a;
}
vector<node> G[maxn];
stack<int> topo;
int nv, ne, ve[maxn] = { 0 }, vl[maxn], indegree[maxn] = { 0 };
bool topoorder() {
    queue<int> q;
    for (int i = 1; i <= nv; i++) {
        for (int j = 0; j < G[i].size(); j++) {
            indegree[G[i][j].v]++;
        }
    }
    for (int i = 1; i <= nv; i++) {
        if (indegree[i] == 0) {
            q.push(i);
            ve[i] = 0;
        }
    }
    while (!q.empty()) {
        int u = q.front();
        topo.push(u);
        q.pop();
        for (int i = 0; i < G[u].size(); i++) {
            indegree[G[u][i].v]--;
            if (ve[G[u][i].v] < ve[u] + G[u][i].w) {
                ve[G[u][i].v] = ve[u] + G[u][i].w;
            }
            if (indegree[G[u][i].v] == 0) q.push(G[u][i].v);
        }
    }
    if (topo.size() != nv) return false;
    else return true;
}
void criticalpath() {
    int max = ve[1], maxid = 1;
    for (int i = 2; i <= nv; i++) {
        if (ve[i] > max) {
            max = ve[i];
            maxid = i;
        }
    }
    cout << max << endl;
    for (int i = 0; i < maxn; i++) vl[i] = max;
    while (!topo.empty()) {
        int u = topo.top();
        topo.pop();
        for (int i = 0; i < G[u].size(); i++) {
            int v = G[u][i].v;
            if (vl[v] - G[u][i].w < vl[u]) {
                vl[u] = vl[v] - G[u][i].w;
            }
        }
    }
    vector<int> keyact[maxn];
    for (int u = 1; u <= nv; u++) {
        for (int i = 0; i < G[u].size(); i++) {
            int v = G[u][i].v, w = G[u][i].w;
            int e = ve[u], l = vl[v] - w;
            if (e == l) keyact[u].push_back(v);
        }
    }
    for (int i = 1; i <= nv; i++) sort(keyact[i].begin(), keyact[i].end(), cmp);
    for (int u = 1; u <= nv; u++) {
        for (int i = 0; i < keyact[u].size(); i++) {
            cout << u << "->" << keyact[u][i] << endl;
        }
    }
}
int main() {
    cin >> nv >> ne;
    int u, v, w;
    for (int i = 0; i < ne; i++) {
        cin >> u >> v >> w;
        G[u].emplace_back(v, w);
    }
    if (!topoorder()) cout << 0;
    else criticalpath();
    return 0;
}

/*
samples:
in:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
out:
17
1->2
2->4
4->6
6->7

in:
4 4
1 2 2
1 3 2
2 4 2
3 4 2
out:
4
1->3
1->2
2->4
3->4

in:
3 3
1 2 1
2 3 1
3 1 1
out:
0

in:
3 3
1 2 1
1 3 1
2 3 1
out:
2
1->2
2->3

*/

Buy me a coffee ? :)
0%