本周课程主要包括图论中最短路径的问题和有关树的习题课,习题课笔记添加到前面对应题目的所在的文章中了。
最短路径问题的抽象
一般而言,最短路径问题都可抽象为:
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径,从而,有:
- 这条路径就是两点之间的最短路径(Shortest Path)
- 第一个顶点为源点(Source)
- 最后一个顶点为终点(Destination)
按照这样的思路,最短路径问题又可以分别两类:
- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径,根据图的类型不同又可以分为:
- (有向)无权图
- (有向)有权图
- 多源最短路径问题:求任意两顶点间的最短路径
无权图的单源最短路径算法
考虑这类问题时,有一个原则,即:按照递增(非递减)的顺序找出各个顶点的最短路。
以下图中的“图”为例: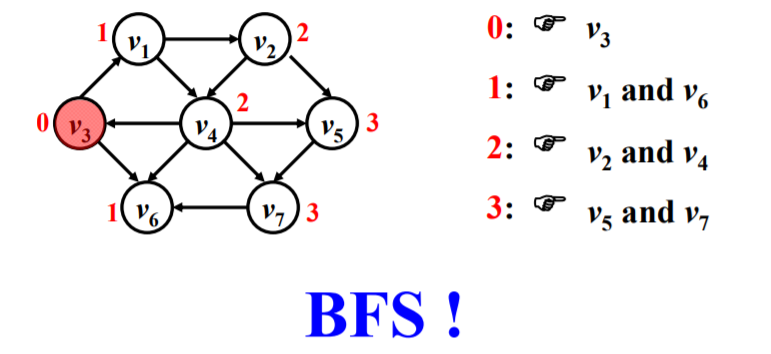
无权图的单源最短路径问题本质上就是 BFS,假设源点为$v_3$,按照 BFS 的思路,通过$v_3$可以直接访问$v_1$和$v_2$,这算是与$v_3$的距离为 1 所能访问的顶点,依次类推,与$V_3$距离为 2 所能访问的顶点就是$v_2$和$v_4$,与$v_3$距离为 3 所能访问的顶点就是$v_5$和$v_7$。
接着在按照 BFS 算法写出其伪码算法:1
2
3
4
5
6
7
8
9
10
11
12
13void Unweighted(Vertex S) {
Enqueue(S, Q);
while(!IsEmpty(Q)) {
V = Dequeue(Q);
for(V 的每个邻接点 W) {
if(dist[W] == -1) {
dist[W] = dist[V] + 1;
path[W] = V;
Enqueue(W, Q);
}
}
}
}
与 BFS 算法不同的是,这里用 dist 数组来保存源点到各个顶点的距离,用 path 数组保存了源点到各个顶点的路径。这里多说一句,若想知道路径的距离是多少直接访问 dist 数组即可;若要知道路径是什么,递归输出 path 数组即可(非递归输出的顺序是逆过来的)。
有权图的单源最短路径
有权图的最短路径与无权图的最短路径最显著的区别就是,有权图的最短路径不一定是进过顶点最少的路径,而无权图的最短路径则一定是经过顶点最少的路径。以下图为例,$v_1 -> v_4 -> v_6$与$v_1 -> v_4 -> v_7 -> v_6$相比,第二条路径要更短一点。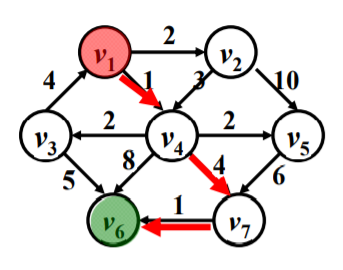
同样,当图内存在负权值的边时,就可能产生负值圈(Negative-cost cycle),如下图: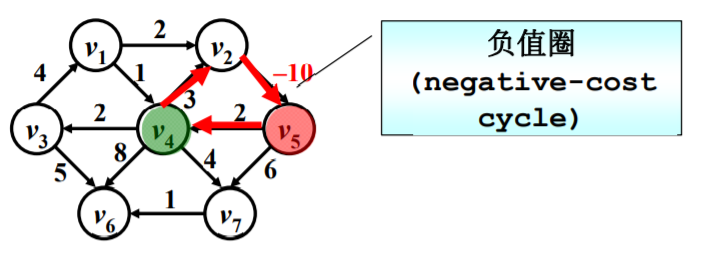
此时单源最短路径的算法是无法得到正确结果的,这里不深入讨论这类问题。
回过头来,有权图的单源最短路径算法与无权图的单源最短路算法有一个共同点,那就是二者皆是按照递增的顺序找出到各个顶点的最短路径,而有权图的单源最短路径算法也叫Dijkstra算法。
Dijkstra 算法
Dijkstra 算法是典型的贪心算法,直接描述其过程有点麻烦,先看下面的伪码算法描述:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void Dijkstra(Vertex S) {
while(1) {
v = 未收录顶点中 dist 最小者;
if(这样的 v 不存在) break;
collected[v] = true;
for(v 的每个邻接点 w){
if(collected[w] == false) {
if(dist[v] + <v, w>的权值 < dist[w]) {
dist[w] = dist[v] + <v, w>的权值;
path[w] = v;
}
}
}
}
}
需要注意的地方:
- 不能解决有负边的情况
- 总是按照顶点序号递增(非递减)的顺序来开始算法
- 每次收录一个顶点 w 后要更新从 v 到 w 的最短路径的权值和
- 每次收录一个顶点 w 后可能会影响 v 到其他顶点的最短路径,所以要对 v 的邻接点进行访问
如何从未收录顶点中找出 dist 最小者是影响此算法时间复杂度的关键,根据方法的不同,有两种情况:
- 直接扫描所有未收录顶点,每次在找出所有顶点中 dist 最小的顶点,然后再访问当前这个顶点的所有邻接点,时间复杂度为:$O(|V^2| + |E|)$,这种方法适合稠密图
- 如果是将 dist 存在最小堆中,那么找出所有顶点中 dist 最小的顶点所耗费的时间就是$O(log|V|)$,但是最后还得将这个值插入到堆中,且对于一个连通的图而言,边数肯定大于等于顶点数,所以其时间复杂度为:$T = O(|V|log|V| + |E|log|V|) = O(|E|log|V|)$,这种方法适合稀疏图
下面再以下图中的图为例,手动模拟一遍算法。
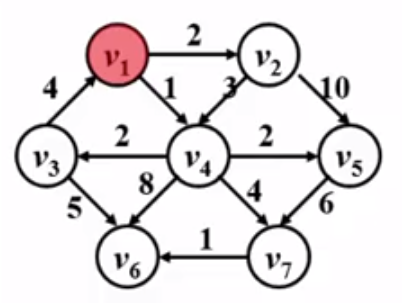
首先,dist 和 path 数组都要先初始化:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| path | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
注意上面下标是从 1 开始的,与顶点下标对应免得搞混,当然从 0 开始也是没有问题的,但后面分析问题时可能搞混淆。
接着从 $v_1$ 开始,在访问$v_1$的邻接点之前,需要先将 dist[1] 的值修改为 0,因为其自身到自身的距离是 0,然后访问$v_1$的邻接点,并更新这些邻接点对应的 dist 和 path 数组的值($v_1$的邻接点只有$v_2$和$v_4$),此时 dist 与 path
数组的值为:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | ∞ | 1 | ∞ | ∞ | ∞ |
| path | -1 | 1 | -1 | 1 | -1 | -1 | -1 |
此时又回到循环体的开头部分,找出 dist 中最小的且未被访问过的,显然是$v_4$,然后利用$v_4$来更新 dist 和 path 数组的值:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | 3 | 1 | 3 | 9 | 5 |
| path | -1 | 1 | 4 | 1 | 4 | 4 | 4 |
再继续下一轮循环,此时选出的顶点就是$v_2$,在更新 dist 和 path 数组的值:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | 3 | 1 | 3 | 9 | 5 |
| path | -1 | 1 | 4 | 1 | 4 | 4 | 4 |
上面表格中的值与第二次循环没有变化,原因在于通过$v_2$并不能使$v_1$到达$v_4$和$v_5$的距离变小,所以也就不用更新 dist 和 path 数组的值。
再继续下一轮循环,此时选出的顶点就是$v_3$(注意是按递增顺序,所以不是$v_5$),此时通过$v_3$可以使$v_1$到$v_6$的距离变小,所以更新数组中的值:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | 3 | 1 | 3 | 8 | 5 |
| path | -1 | 1 | 4 | 1 | 4 | 3 | 4 |
接着选定$v_5$,按照同样的过程,数组值也不用更新。
在选定$v_7$,此时可以使$v_1$到$v_6$的距离变小,更新数组的值:
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | 3 | 1 | 3 | 6 | 5 |
| path | -1 | 1 | 4 | 1 | 4 | 7 | 4 |
最后一个顶点是$v_6$,但$v_6$没有邻接点(就算有,此时其他顶点也都被访问过了),所以循环会结束。
注意上述过程与姥姥讲的略微有点不一致,也就是开头加入$v_1$后,数组值都是循环体内更新的;而姥姥讲的是在循环开始之前就已经全部更新好了。实际上,在循环体内更新还要更加方便一点。
有权图的多源最短路径
考虑有权图的多源最短路径时,毫无疑问会想到直接将单源最短路径算法调用$|V|$(因为顶点个数是$|V|$),此时算法的时间复杂度为:$ T = O(|V^3| + |E| \times |V|)$,显然如果是稀疏图,效率较高。
那碰到稠密图怎么办呢?答案是用 Floyd 算法
Floyd 算法
Floyd 算法与 Dijkstra 算法有点类似,但是其借助了数学归纳法,相比 Dijkstra 算法,代码要简单一点。
注意 Floyd 算法只能用于邻接矩阵,它本身也是通过邻接矩阵来更新最短路径的权值之和的,当$D^{k-1}$已经完成,递推到$D^k$时,主要理解两个点:
- 若 k 不在最短路径$i -> \dots -> j$之间,则$D^k = D^{k-1}$
- 若 k 在最短路径径$i -> \dots -> j$之间,则该路径必定由两段最短路径组成:$D^k[i][j] = D^{k-1}[i][k] + D^{k-1}[k][j]$
其伪码描述为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19void Floyd() {
for(i = 0; i < N; i++) {
for(j = 0; j < N; j++) {
D[i][j] = G[i][j]; // initialization
path[i][j] = -1;
}
}
// notice these loop variables
for(k = 0; k < N; k++) {
for(i = 0; i < N; i++) {
for(j = 0; j < N; j++) {
if(D[i][k] + D[k][j] < D[i][j]) {
D[i][j] = D[i][k] + D[k][j];
path[i][j] = k;
}
}
}
}
}
Homework
07-4 哈利·波特的考试
这道题目是典型的多源最短路径问题,直接用邻接矩阵存储图,然后调用 Folyd 算法即可得到所有的最短路径。但要注意这道题目的最优解是选择出到其他各顶点的综合距离最短的顶点,也就是说各个顶点到其他顶点的最短路径中最长的那条最短路径的最小值者就是最优解,好吧,很拗口。注意,并不能以最短路径之和最小者为最优解,这是错误的。
这道题的代码写的比较简单,思路与上述一致,如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
using namespace std;
const int maxn = 100 + 5;
const int inf = 0x3fffffff;
int n, m, G[maxn][maxn], dist[maxn][maxn];
void floyd() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
dist[i][j] = G[i][j];
}
}
for(int k = 1; k <= n; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(dist[i][k] + dist[k][j] < dist[i][j] && i != j) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
void findanimal() {
floyd();
int mindist = inf;
int animal;
for(int i = 1; i <= n; i++) {
int maxdist = 0;
for(int j = 1; j <= n; j++) {
if(i != j && dist[i][j] > maxdist) maxdist = dist[i][j];
}
if(maxdist == inf) {
cout << 0;
return;
}
if(mindist > maxdist) {
mindist = maxdist;
animal = i;
}
}
cout << animal << ' ' << mindist;
}
int main() {
fill(G[0], G[0] + maxn * maxn, inf);
cin >> n >> m;
int v1, v2;
for(int i = 0; i < m; i++) {
cin >> v1 >> v2;
cin >> G[v1][v2];
G[v2][v1] = G[v1][v2];
}
findanimal();
return 0;
}
/*
samples:
in:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
out:
4 70
*/
07-5 Saving James Bond - Hard Version
这道题目是上周题目的加强版,题目大意与姥姥在课上开头讲的一样,不仅要判断是否可以到达岸边,还要输出对应的路径。
解决这个问题的思路就是利用 BFS 算法来找最短路径,也就是无权图的单源最短路径。可能有的同学会觉得顶点之前的距离不就是边的权吗?其实不然,这个题目的边权不是直接给出,需要计算得到;而且,这个题目的最优解不是要求最短路径的权值最小,而是要求跳的次数最少,所以,只需要用计算出边权然后判断是否可达即可。
要求得具体经过了几跳到达岸边,稍微有点麻烦,但可以借鉴上篇文章六度空间那个题目的思路,在开始 BFS 之前先记录是哪个顶点,在每次循环结束之前,将当前加入路径的结点与记录的结点比对,如果相同,那么跳步数加 1,并将此结点记录后用作下轮循环判断。
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
using namespace std;
const int maxn = 100 + 5;
struct node {
int x, y;
} coords[maxn];
int n, d, path[maxn];
bool vis[maxn] = {false};
int firstjump(int v) {
int dis = d - sqrt(pow(coords[v].x, 2) + pow(coords[v].y, 2)) + 7.5;
if(dis > 0) return dis;
else return 0;
}
bool jump(int v, int w) {
return sqrt(pow(coords[v].x - coords[w].x, 2) + pow(coords[v].y - coords[w].y, 2)) <= d;
}
bool issafe(int v) {
return fabs(fabs(coords[v].x) - 50) <= d || fabs(fabs(coords[v].y) - 50) <= d;
}
bool cmp(int a, int b) {
return firstjump(a) > firstjump(b);
}
void printpath(int inde) {
if(path[inde] == -1) {
cout << coords[inde].x << ' ' << coords[inde].y << endl;
return;
}
printpath(path[inde]);
cout << coords[inde].x << ' ' << coords[inde].y << endl;
}
void save007() {
if(d >= 50 - 15 / 2) {
cout << 1;
return;
} else {
int order[maxn];
queue<int> q;
for(int i = 0; i < n; i++) {
order[i] = i;
path[i] = -1;
}
sort(order, order + n, cmp);
int last, tail;
for(int i = 0; i < n; i++) {
if(firstjump(order[i])) {
q.push(order[i]);
vis[order[i]] = true;
last = order[i];
}
}
int step = 2;
while(!q.empty()) {
int front = q.front(); q.pop();
if(issafe(front)) {
cout << step << endl;
printpath(front);
return;
}
for(int i = 0; i < n; i++) {
if(!vis[i] && jump(front, i)) {
q.push(i);
path[i] = front;
vis[i] = true;
tail = i;
}
}
if(last == front) {
step++;
last = tail;
}
}
if(q.empty()) cout << 0;
}
}
int main() {
cin >> n >> d;
for(int i = 0; i < n; i++) {
cin >> coords[i].x >> coords[i].y;
}
save007();
return 0;
}
/*
samples:
in:
17 15
10 -21
10 21
-40 10
30 -50
20 40
35 10
0 -10
-25 22
40 -40
-30 30
-10 22
0 11
25 21
25 10
10 10
10 35
-30 10
out:
4
0 11
10 21
10 35
in:
4 13
-12 12
12 12
-12 -12
12 -12
out:
0
in:
1 50
30 30
out:
1
*/
07-6 旅游规划
这道题目是中文的,读起来没那么费劲了,所以很容易让人看出是单源最短路径问题。
题目已经给定了源点和终点,所以用源点直接套 Dijkstra 算法即可得到其到终点的最短路径。
但这个题目的难点在于要根据题目给定的选解方式来确定最优解,即:
- 路径最短
- 最便宜
所以需要修改一下 Dijkstra 算法,具体代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61/* notes: this problem is similar to the Advanced Level 1030. */
using namespace std;
const int inf = 0x3fffffff;
const int maxn = 500 + 5;
int n, m, src, dst, G[maxn][maxn], cost[maxn][maxn];
int d[maxn], c[maxn];
bool vis[maxn] = {false};
void dijkstra(int src) {
fill(d, d + maxn, inf);
d[src] = 0;
c[src] = 0;
for(int i = 0; i < n; i++) {
int v = -1, min = inf;
for(int j = 0; j < n; j++) {
if(!vis[j] && d[j] < min) {
v = j;
min = d[j];
}
}
if(v == -1) return;
vis[v] = true;
for(int w = 0; w < n; w++) {
if(!vis[w] && G[v][w] != inf) {
if(d[v] + G[v][w] < d[w]) {
d[w] = d[v] + G[v][w];
c[w] = c[v] + cost[v][w];
} else if(d[v] + G[v][w] == d[w]) {
if(c[v] + cost[v][w] < c[w]) c[w] = c[v] + cost[v][w];
}
}
}
}
}
int main() {
fill(G[0], G[0] + maxn * maxn, inf);
cin >> n >> m >> src >> dst;
int v1, v2;
for(int i = 0; i < m; i++) {
cin >> v1 >> v2;
cin >> G[v1][v2] >> cost[v1][v2];
G[v2][v1] = G[v1][v2], cost[v2][v1] = cost[v1][v2];
}
dijkstra(src);
cout << d[dst] << ' ' << c[dst];
return 0;
}
/*
samples:
in:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
out:
3 40
*/

